Wie alles begann: Eine kurze Geschichte der komplexen Zahlen

Als Schöpfer der komplexen Zahlen ging Geronimo (oder Gerolamo) Cardano (1501-1576) in die Geschichte der Mathematik ein. In jener Zeit war es unter Gelehrten üblich, ihr Wissen in Schaukämpfen unter Beweis zu stellen. Dies war häufig eine gute Geldeinnahmequelle und bot auch die Möglichkeit, eine Professur an einer Universität zu bekommen. Die Veröffentlichung von akademischen Ergebnissen war daher unüblich, man behielt seine Erkenntnisse für sich, um möglichst viel Profit daraus zu schlagen. Die mathematische Forschung im 16. Jahrhundert beschäftigte sich besonders mit der Lösung von polynomialen Gleichungen.

In einem Wettkampf im Jahre 1530 gelang es Niccolo Tartaglia, eine Formel für die Lösung spezieller kubischer Gleichungen herzuleiten. Nach langem Drängen Cardanos gab Tartaglia ihm schließlich die Formel preis und Cardano veröffentlichte dieses Ergebnis einige Jahre später. Cardano verallgemeinerte Tartaglia's Formel und verwendete dazu negative Zahlen, die damals noch als rätselhaft angesehen wurden, und darüber hinaus sogar ihre Wurzeln. Dadurch konnte er geschlossene Lösungsformeln für alle quadratischen und kubischen Gleichungen angeben, ein Ergebnis, das er 1545 erstmals veröffentlichte.

Cardano beließ es bei der Entdeckung solcher komplexen Zahlen, die ihm genauso "subtil wie nutzlos" erschienen. Allgemeine Regeln für das Rechnen mit Wurzeln negativer Zahlen wurden dann erst einige Jahre später von Rafael Bombelli aufgestellt und erfolgreich in der Cardanoschen Formel angewendet.

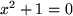Das Symbol für die imaginäre Einheit als Lösung von wurde erstmals 1777 von Leonhard Euler (1707-1783) eingeführt. Von ihm stammt auch die sogenannte Eulersche Formel:

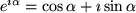
Für ergibt sich eine der schönsten mathematischen Beziehungen:

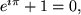
die einen erstaunlichen Zusammenhang zwischen den Fundamentalzahlen 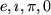und herstellt.

Damit waren die mysteriösen komplexen Zahlen aber immer noch nicht hinreichend erklärt. Erst Carl Friedrich Gauß (1777-1855) gelang 1831 eine geometrische Interpretation der komplexen Zahlen, indem er sie als Punkte in einer Ebene auffasste und so den Begriff der Gaußschen Zahlenebene prägte. Sechs Jahre später konnte William R. Hamilton (1805-1865) ihnen auch eine arithmetische Einkleidung geben. Seitdem sind die komplexen Zahlen aus der Mathematik und ihren Anwendungswissenschaften nicht mehr wegzudenken.

Literatur: H. Heuser: Lehrbuch der Analysis, Teil 1