Beispiel zur Konvergenz
Beispiel:
Die Folge
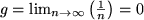 Beweis: Zu beliebigem 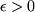 wähle
wähle
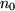 als kleinste ganzzahlige Zahl, die
als kleinste ganzzahlige Zahl, die
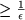 ist. Dann folgt für alle
ist. Dann folgt für alle
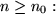
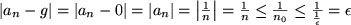 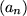 konvergent und hat den Grenzwert g = 0.
konvergent und hat den Grenzwert g = 0.
Erklärungen zum Beweis: Um zu beweisen, dass die Folge den Grenzwert g = 0 hat, muss die in der Definition des Grenzwertes angegebene Eigenschaft bewiesen werden. Dazu muss aber schon die Vermutung vorliegen, wie der Grenzwert lautet. Im allgemeinen bekommt man eine solche Vermutung, indem man große Werte für n einsetzt, um zu sehen an welchen Wert sich die Folge annähert. Bei zusammengesetzten Folgen sind die Rechenregeln für Grenzwerte hilfreich. Hat man nun die Vermutung g = 0 aufgestellt, braucht man für den Beweis noch einen passenden Wert für 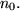 Dazu beginnt man, wie in der Definition angegeben,
Dazu beginnt man, wie in der Definition angegeben,
 zu berechnen, und kommt auf
zu berechnen, und kommt auf
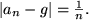 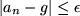 nur für alle
nur für alle
 bewiesen werden soll, gilt
bewiesen werden soll, gilt
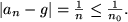 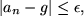 gilt, wenn
gilt, wenn
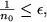 also
also
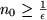 gilt. Da
gilt. Da
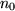 ganzzahlig sein muß, wählt man also die kleinste ganzzahlige Zahl größer als
ganzzahlig sein muß, wählt man also die kleinste ganzzahlige Zahl größer als
 und der Beweis ist vollständig.
und der Beweis ist vollständig.
|
1 Anmerkung:
Da die Ungleichung für jedes
|
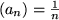 ist konvergent und besitzt den Grenzwert
ist konvergent und besitzt den Grenzwert
 gelten soll, hängt
gelten soll, hängt
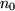 oft von
oft von
 ab.
ab.