Motivation und Experiment

Für die Analysis ist der Begriff des Grenzwertes grundlegend. In diesem Kapitel werden Folgen und ihre Grenzwerte eingeführt. Damit ist es anschließend möglich, wichtige Begriffe wie die Stetigkeit und Differenzierbarkeit von Funktionen, das Integral als Grenzwert von Ober- und Untersummen, sowie die Konvergenz von unendlichen Reihen zu definieren.

Betrachten Sie die rekursive Entstehung der geometrischen Figuren im folgenden Applet. Überlegen Sie, nach welcher Gesetzmäßigkeit die jeweils nächste Figur entsteht. Beobachten Sie die jeweilige Kantenlänge und den Flächeninhalt, von Schritt zu Schritt.

Was geschieht mit der Kantenlänge bzw. dem Flächeninhalt wenn man die Figur nicht nur bis zum zehnten oder zwölften Schritt betrachtet, sondern immer weiter bis ins Unendliche? Werden auch sie unendlich groß, oder gibt es vielleicht eine Grenze, die sie nie überschreiten? Obwohl sich die Figuren auf den ersten Blick recht ähnlich sehen, ist ihr Verhalten auf diese Frage bezogen sehr unterschiedlich.

Quadratpflanze

Hier wird die Kantenlänge offensichtlich in jedem Schritt um zwei größer. Sie ist also nicht beschränkt, sondern wächst ins Unendliche, wenn man die Figur immer weiter aufbaut. Der Flächeninhalt dagegen nähert sich immer weiter an den Wert 1,5 an und wird diesen nie überschreiten. Die Quadratpflanze wird also zu einer Figur, die unendliche Kantenlänge, aber einen endlichen Flächeninhalt besitzt.

Sierpinski-Dreiecke

Es wird mit einem Dreieck mit Flächeninhalt 1 begonnen. In jedem Schritt wird jedes Dreieck in der Figur in vier kleinere Dreiecke aufgetailt und das jeweils mittlere entfernt. Hier ist das bei der Quadratpflanze beobachtete Verhalten sogar noch extremer: Ist der Flächeninhalt im ersten Schritt 1, so wird er in jedem Schritt auf 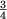seiner vorherigen Größe reduziert. Wie wir später noch sehen werden bedeutet das, dass sich der Flächeninhalt mit wachsender Anzahl Schritte immer mehr der Null annähert. Die Kantenlänge dagegen wächst, wie bei der Quadratpflanze, ins Unendliche. Bei "unendlicher Anzahl Schritte" bekämen wir also eine Figur mit unendlicher Kantenlänge, aber Flächeninhalt Null!

Baum des Pythagoras

Nach dem Satz des Pythagoras haben die beiden im ersten Schritt hinzukommenden Quadrate zusammen genau den gleichen Flächeninhalt, wie das Ursprungsquadrat. Ebenso haben in jedem weiteren Schritt die neuen Quadrate insgesamt denselben Flächeninhalt, wie die Quadrate des vorherigen Schritts aus denen sie entstanden sind. Der Flächeninhalt wächst also in jedem Schritt um den Inhalt des Anfangsquadrates und wird somit unendlich groß. Die Kantenlänge des Baumes geht ebenfalls gegen unendlich.

Die Berechnung solcher "Grenzwerte" von Zahlenfolgen ist Gegenstand der folgenden Kapitel.