Konvergenz von Folgen und Häufungspunkte
Definition: Grenzwert
Die Zahl g heißt Grenzwert der Folge
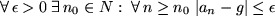 |
1 Anmerkung:
Mit Hilfe dieser formalen Definition läßt sich beweisen, dass g der Grenzwert der Folge ist.
Für das praktische Rechnen ist sie aber unbrauchbar, da sie keinen Grenzwert liefert, sondern sich mit ihr nur bereits
vermutete Grenzwerte überprüfen lassen.
|
2 Anmerkung:
Die natürliche Zahl
|
3 Anmerkung:Man kann zeigen, dass eine Folge höchstens einen Grenzwert besitzen kann. |
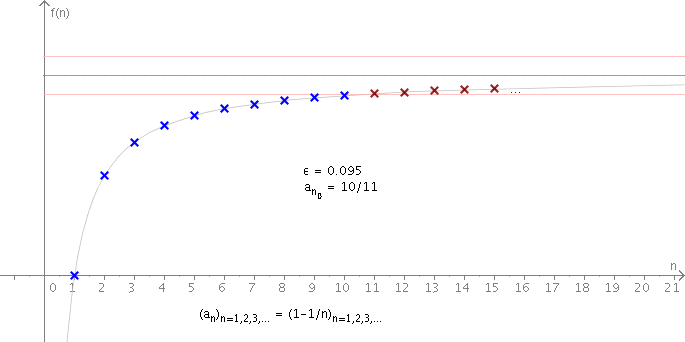
Veranschaulichung
Besitzt eine Folge
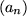 den Grenzwert g, so liegen für ein
den Grenzwert g, so liegen für ein
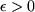 alle Folgenglieder
alle Folgenglieder
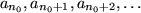 innerhalb der Umgebung mit Abstand
innerhalb der Umgebung mit Abstand
 von g:
von g:
Definition: KonvergenzEine Folge heißt konvergent, wenn sie einen Grenzwert g hat. Symbolische Schreibweise: 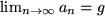 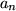 für n gegen unendlich gleich g)
für n gegen unendlich gleich g)
Eine Folge heißt divergent, wenn sie nicht konvergent ist, d.h. wenn sie keinen Grenzwert besitzt. |
Der folgende Satz liefert ein Kriterium für die Konvergenz einer Folge, auch ohne dass eine Vermutung über einen konkreten Grenzwert vorliegt:
4 Satz: Konvergenzkriterium von Cauchy
Die Folge
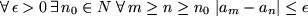 |
Anschaulich gesprochen heißt das, für jede noch so kleine Zahl
 gibt es einen Index
gibt es einen Index
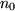 , ab dem alle weiteren Folgenglieder höchstens den Abstand
, ab dem alle weiteren Folgenglieder höchstens den Abstand
 voneinander haben.
voneinander haben.
Definition: Häufungspunkt
Eine Zahl a ist Häufungspunkt einer Folge
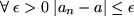 |
Also ist a Häufungspunkt von
 wenn es für jede noch so kleine Zahl
wenn es für jede noch so kleine Zahl
 unendlich viele Folgenglieder gibt, die höchstens den Abstand
unendlich viele Folgenglieder gibt, die höchstens den Abstand
 von a haben.
von a haben.
5 Satz: Satz von Bolzano Weierstraß
Jede beschränkte Folge
|
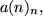 wenn es für jede noch so kleine Epsilon-Umgebung von g einen Index
wenn es für jede noch so kleine Epsilon-Umgebung von g einen Index
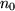 gibt, ab dem alle Folgenglieder in dieser Epsilon-Umgebung liegen:
Symbolische Schreibweise:
gibt, ab dem alle Folgenglieder in dieser Epsilon-Umgebung liegen:
Symbolische Schreibweise:
 hängt i.a. von der Wahl der Zahl
hängt i.a. von der Wahl der Zahl
 ab. Man schreibt daher auch
ab. Man schreibt daher auch
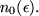
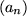 ist konvergent genau dann, wenn
ist konvergent genau dann, wenn
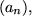 wenn für unendlich viele
wenn für unendlich viele
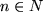 gilt:
gilt:
 besitzt mindestens einen Häufungspunkt
besitzt mindestens einen Häufungspunkt