Beispiel zu Divergenz und Häufungspunkten
Beispiel:
Die Folge
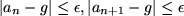  Es würde folgen:
Es würde folgen:
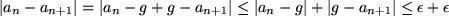 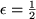 folgt daher:
folgt daher:
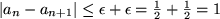 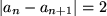 Somit ist die Annahme, dass ein Grenzwert g existiert, falsch. Die Folge 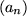 ist nicht konvergent.
Sie besitzt zwei Häufungspunkte:
ist nicht konvergent.
Sie besitzt zwei Häufungspunkte:
Für n gerade: 1 Für n ungerade: -1 Erklärungen zum Beweis: Es soll bewiesen werden, dass kein Grenzwert existiert. Also muss für einen beliebigen angenommenen Grenzwert g ein Widerspruch herbeigeführt werden. Anschaulich ist klar, dass die Folge nicht auf einen Wert zuläuft. Man sieht sofort, daß für jedes  gilt. Die Definition des Grenzwertes beruht darauf, daß die Folgenglieder immer näher an einen bestimmten Wert
kommen. Da dies bei unserer Folge nicht der Fall ist, versuchen wir dies auszunutzen und die Formel aus
der Definition mit der obigen Formel in Verbindung zu setzen. Also
gilt. Die Definition des Grenzwertes beruht darauf, daß die Folgenglieder immer näher an einen bestimmten Wert
kommen. Da dies bei unserer Folge nicht der Fall ist, versuchen wir dies auszunutzen und die Formel aus
der Definition mit der obigen Formel in Verbindung zu setzen. Also
  ein
ein
 so dass für jedes
so dass für jedes
 gilt
gilt
 Damit folgt aus obiger Formel also
Damit folgt aus obiger Formel also
  Dies kann natürlich nicht stimmen, wie die Wahl von
Dies kann natürlich nicht stimmen, wie die Wahl von
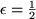 zeigt, und wir haben einen Widerspruch herbeigeführt.
zeigt, und wir haben einen Widerspruch herbeigeführt.
|
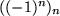 ist divergent. Sie besitzt zwei Häufungspunkte: 1, -1
ist divergent. Sie besitzt zwei Häufungspunkte: 1, -1
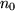 existieren mit:
existieren mit: