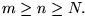Konvergenz von Reihen
Definition: Konvergenz und Divergenz
Eine unendliche Reihe
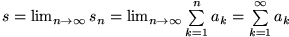 Eine unendliche Reihe heißt divergent , falls die Folge ihrer Partialsummen keinen Grenzwert s hat. Ist s  oder
oder
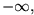 so heißt die Reihe auch bestimmt divergent .
so heißt die Reihe auch bestimmt divergent .
Eine unendliche Reihe heißt absolut konvergent , wenn die Partialsummenfolge der Beträge 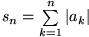 konvergiert.
konvergiert.
|
-
Die Konvergenz bzw. Divergenz einer unendlichen Reihe kann man formal mit Hilfe der Konvergenzkriterien bestimmen.
-
Eine konvergente Reihe besitzt stets eine endlichen, eindeutig bestimmten Summenwert.
-
Eine absolut konvergente Reihe ist stets konvergent. Die Umkehrung gilt nicht. (Gegenbeispiel ist
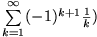
1 Satz: Cauchybedingung für Reihenkonvergenz
Die Reihe
|
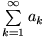 heißt konvergent, wenn die Folge
heißt konvergent, wenn die Folge
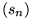 ihrer Partialsummen den Grenzwert s besitzt:
ihrer Partialsummen den Grenzwert s besitzt:
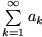 konvergiert genau dann, wenn es zu jedem
konvergiert genau dann, wenn es zu jedem
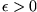 ein
ein
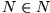 gibt, so dass
gibt, so dass
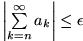 für alle
für alle