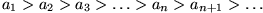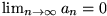Konvergenzkriterien

Notwendiges Konvergenzkriterium:

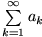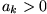Wenn die Reihe mit konvergiert, so muss 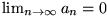gelten, d.h. ihre Glieder müssen eine Nullfolge bilden. Diese Bedingung ist notwendig (d.h. damit die Reihe konvergiert, muss sie erfüllt sein) aber nicht hinreichend (d.h. es ex. divergente Reihen, deren Glieder eine Nullfolge bilden).

Hinreichende Konvergenzkriterien:

Zur Bestimmung der Konvergenz bzw. Divergenz einer Reihe kann man eines der folgenden Kriterien anwenden:

• Wurzelkriterium:
  
  Es sei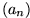 eine beliebige Folge. Dann gilt:

  1. Existiert ein q mit 0 < q < 1, so dass für jedes n gilt: 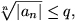dann ist 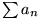absolut konvergent.

  2. Gilt 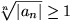für alle n, dann ist 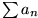divergent.

• Quotientenkriterium:
  
  Wenn die Glieder der unendlichen Reihe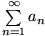 die Bedingung

  erfüllen, so ist die Reihe konvergent. Ist aber q > 1, so ist die Reihe divergent. Für q=1 versagt das Quotientenkriterium gänzlich und es muss ein anderes Konvergenzkriterium angewendet werden.
  
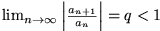
  ACHTUNG: Das Quotientenkriterium ist eine hinreichende Bedingung für die Konvergenz von Reihen, allerdings keine notwendige! Es gibt also Reihen, die keinen Grenzwert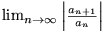 haben und dennoch konvergieren.

• Leibnizkriterium (für alternierende Reihen):
  
  Liegt eine alternierende Reihe von der Form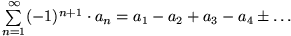 mit 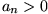vor, so ist diese konvergent, wenn folgende zwei Bedingungen erfüllt sind:

  1. 

  2. 

• Majoranten-Minoranten-Kriterium:
  
  Es seien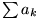 und 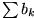Reihen mit nicht-negativen Gliedern.
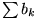  ist eine Majorante von 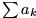genau dann, wenn 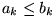für alle k gilt. Umgekehrt wird 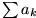Minorante von 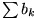genannt.

  1. Ist dann 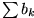konvergent, so ist auch 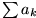konvergent.

  2. Ist 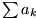divergent, so ist auch 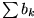divergent.

• Integralkriterium
  
  Lassen sich die Glieder einer Reihe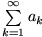 mit positiven Gliedern als Funktionswerte 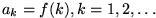einer im Intervall 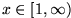stetigen, monoton fallenden Funktion f(x) darstellen, so gilt:

  1. konvergiert 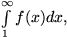so konvergiert auch

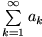
  2. divergiert 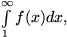so divergiert auch
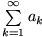