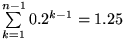Einführendes Beispiel
Im Folgenden werden die Begriffsbildungen um unendliche Reihen anhand eines konkreten Zahlenbeispiels entwickelt.
Betrachten Sie die unendliche Zahlenfolge
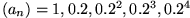

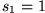
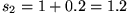
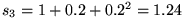
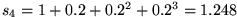

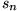 bilden wiederum eine Folge, nämlich
bilden wiederum eine Folge, nämlich
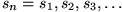 mit dem Bildungsgesetz
mit dem Bildungsgesetz
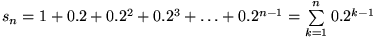
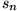 heißt dabei die n-te Partialsumme, d.h. die Summe der ersten n Glieder der
Zahlenfolge
heißt dabei die n-te Partialsumme, d.h. die Summe der ersten n Glieder der
Zahlenfolge
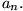 Für die Partialsummenfolge
Für die Partialsummenfolge
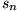 wird die Bezeichnung Unendliche Reihe eingeführt und
symbolisch geschrieben
wird die Bezeichnung Unendliche Reihe eingeführt und
symbolisch geschrieben
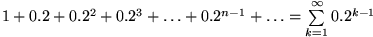
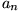 interpretiert werden. Es stellt sich die Frage, ob eine solche unendliche
Reihe einen "Summenwert" hat, der für endliche Reihen ja einfach ausgerechnet
werden kann. Bei unendlichen Reihen wird dagegen der Grenzwert der
Partialsummenfolge
interpretiert werden. Es stellt sich die Frage, ob eine solche unendliche
Reihe einen "Summenwert" hat, der für endliche Reihen ja einfach ausgerechnet
werden kann. Bei unendlichen Reihen wird dagegen der Grenzwert der
Partialsummenfolge
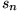 (sofern er existiert) als Summenwert definiert.
In dem obigen Zahlenbeispiel muss daher untersucht werden, ob der Grenzwert
(sofern er existiert) als Summenwert definiert.
In dem obigen Zahlenbeispiel muss daher untersucht werden, ob der Grenzwert
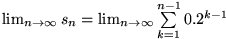
Dafür betrachten wir die beiden Darstellungen von
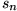
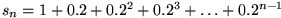
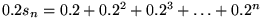
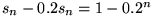
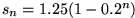
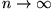 gilt
gilt
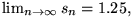 da
da
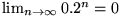 ist.
ist.
Die obige unendliche Reihe hat damit den Summenwert 1.25 und man schreibt symbolisch